
主要基于李宏毅老师的讲解,结合了李沐老师的观点。
“归一化”实际上是错误的称呼,数学上正确的术语是“标准化”。奈何「学深度学习那帮人数学不好」——沐神
前情提要#
在 backward 的时候,上层(靠近输出)的梯度一般较大,更新快;下层(靠近输入)的梯度一般较小,更新慢。这就导致了模型的短视问题(上层积极拟合,对当前 batch 拟合好,但泛化较差)和失忆问题(下层一旦更新,上层需要重新学习,形成了震荡,又称 Internal Covariant Shift;学习率越大,这种震荡越明显)。此事在[[数值稳定性#梯度消失]] 中亦有记载。
Dropout 一定程度上也是为了减轻这个问题:在靠近输出的全连接层后面放置 Dropout(Dropout 的常用实践),可以抑制上层过拟合当前 batch,变相地允许下层受到更多更新、学习到更多 feature(不被上层抢着学掉了)。
而 BatchNorm,主要就是用来解决这个问题。
批量归一化#
BatchNorm 能将靠近输出的层和靠近输入的层的训练过程一定程度上解耦。让下层更新时,上层已经学习到的权重不会完全失效、需要重新学习。也就是说,它解决了前情提要中下划线部分描述的问题。
不建议在同一层的后面串联使用 BatchNorm 和 Dropout。这是因为 BatchNorm 已经具有了正则化效果(batch-level 噪声),叠加 Dropout 效果不明显;且 Dropout 会影响 BatchNorm 对样本均值/方差的估计。
但是,同一个网络中的不同位置是可以同时使用 BatchNorm 和 Dropout 的,尤其是像前情提要中提到的“在高层全连接层后放置 Dropout”,仍然是被推荐的。究其本质,BatchNorm 和 Dropout 虽然都有正则的作用,但生态位不完全重合,前者是减轻“失忆”,后者是减轻“短视”。
具体操作#
BatchNorm 层具有两个可学习参数:目标均值 和目标标准差 .
配合全连接层#
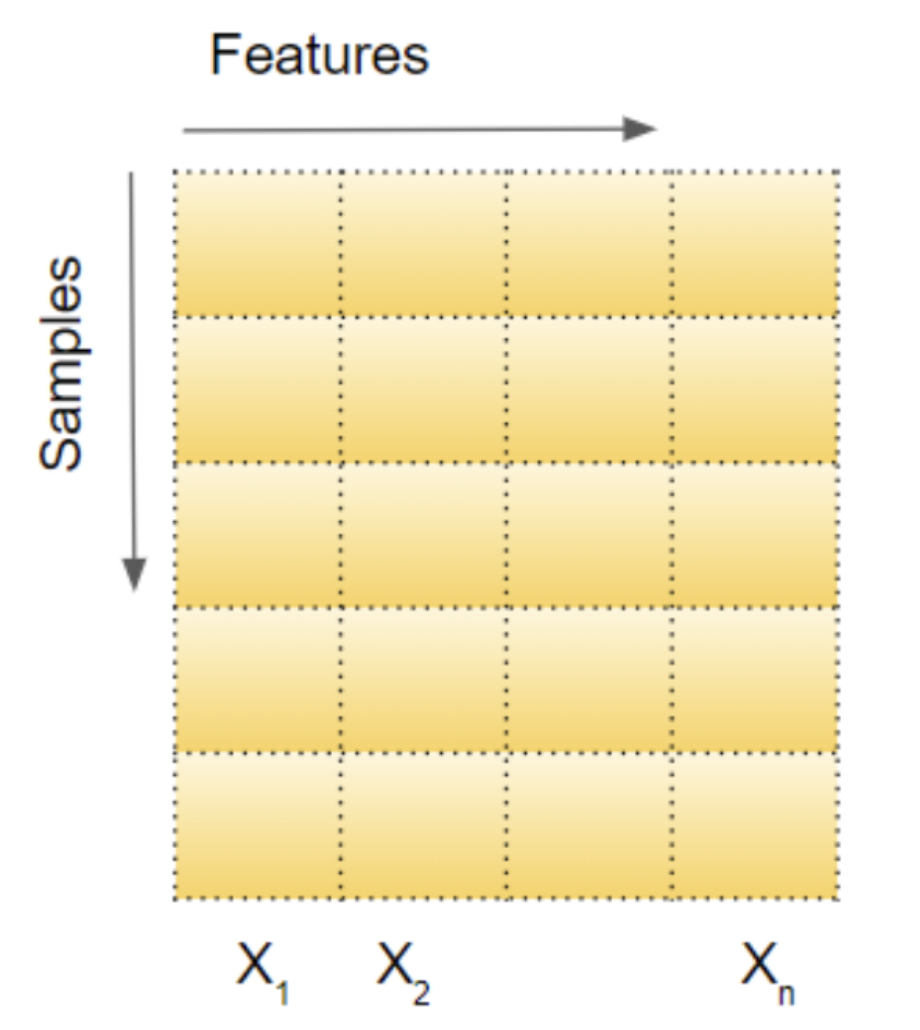
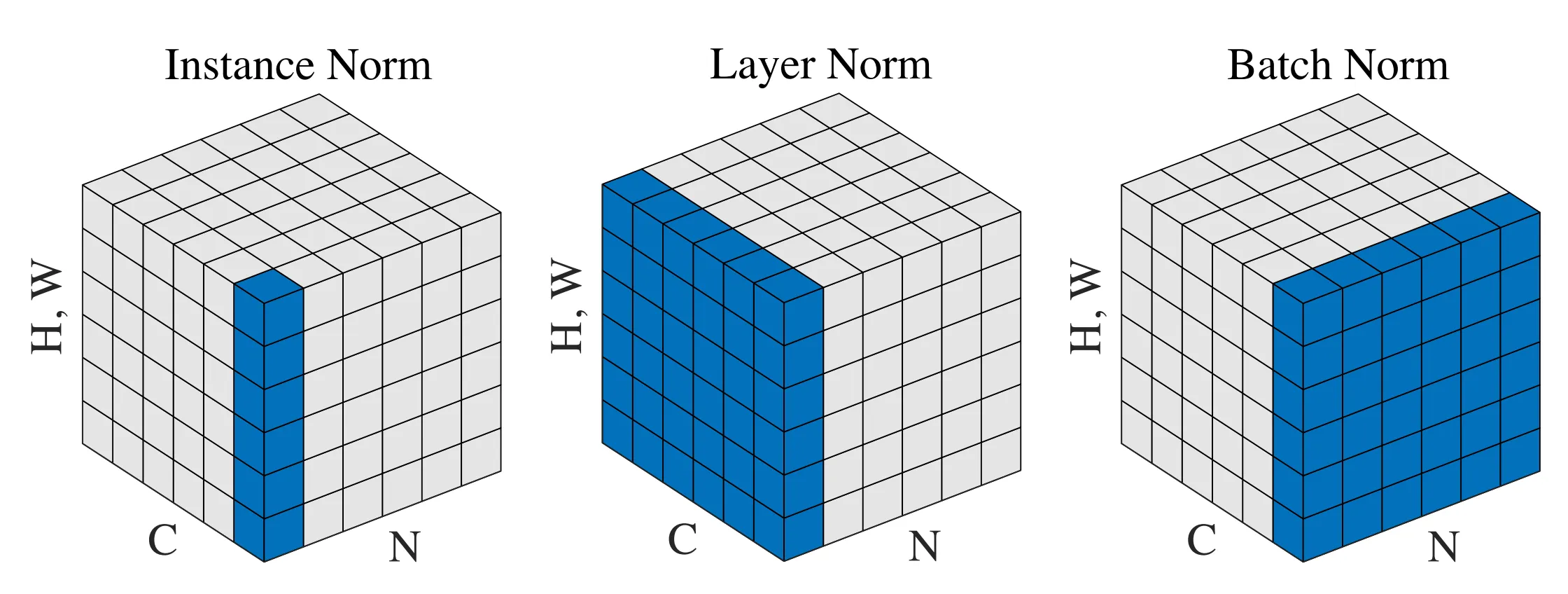
对于全连接层来说(输入输出是 batch_size 个行向量组成的矩阵),BatchNorm 会对当前的输入在 samples 维度上计算均值 和标准差 ,算出来的 和 都是和 feature 长度相同的向量。然后将每个 sample 的数值进行如下变换 ,其中向量之间的减法和除法都是逐元素的,因此归一化对于每一个 sample 的不同 feature 元素是平行的,每个 feature 都和整个 batch 里面所有其它 sample 的同一个位置的 feature 做归一化,在上图中就是每一列单独归一化为满足那一列的均值 标准差 的 distribution.
通常来说,BatchNorm 会放在全连接层和激活函数之间(归一化输出),或者全连接层之前(归一化输入)。紧挨着放在激活函数之后的做法较少见(可能是将激活函数的值域归一化,不如直接改激活函数?)。
配合卷积层#
大体上和全连接层类似。只不过只作用在输入的通道维上。具体来说,请想象一张 feature map,它有 CHW 三个维度,把每个像素(一个向量,这个向量的长度就是通道数)拿出来成为一个行向量,把一个 feature map 变成行向量堆叠成的矩阵;
对于一个 batch,会有多个上述的矩阵,把它们也全都堆叠起来,得到一个 batch 里面每一个 sample 的所有像素直接堆叠起来的大矩阵,然后按照类似全连接层中的处理方法即可。
细节#
在做 Inference 的时候,比如 Eval 或者 Test,很可能输入不再是一个 Batch 而只是单个 sample,这个时候 和 无法计算(如果直接取 = sample, = 0 可能会导致输出不稳定),因此 Batch Norm 的做法是,在训练的过程中逐步统计、近似算出整个 training dataset 上的 和 ,然后直接将这个 和 拿到 Inference 的时候进行归一化。
在训练的时候,方差 会被加上一个小的正数 (一般取 1e-5)再开方,以防止 过于接近 0 而导致 0/0 问题。 一般不会取太小,否则没有效果;也不能取太大,否则在分母上喧宾夺主了。修改后的式子是:
好处#
- 抑制 Covariant Shift(此处李沐指出实际上并不存在),从而允许增大学习率加快训练
- 对于不同的 feature 维度,有的绝对值大,有的绝对值小,使用统一的学习率会导致有的维度震荡、有的维度步长过小,而为每个维度设置不同的学习率过于麻烦;这时候如果使用 BatchNorm,会让整体的梯度更加集中,或者说让「Error Surface」(李宏毅的说法)更加平坦,从而允许使用统一的、较大的学习率。
- 将每一层的 feature fit 到适合激活函数的区间,可以防止落在激活函数(以 Sigmoid 为首)的饱和区域从而出现梯度消失
- 降低模型对初始化的敏感程度
- 有一定抑制 overfitting 的作用,相当于给数据降噪(和李沐的观点——增加噪音——相反),让网络重点关注随不同 batch 变化不大的趋势(一般式真实规律),而忽略每个 batch 自身的噪声。
注意:Batch Norm 被证明不会显著提升模型的最终精度(李沐的观点)。
用了 Batch Norm,要记得加大学习率,不然发挥不出加速收敛的作用!